
2026-02-17 11:37:39

2
文章摘要:杯赛单场淘汰制因其偶然性强、悬念突出而成为竞技体育中最具观赏价值的赛制之一,其中“弱胜强”的爆冷现象尤为引人关注。本文以杯赛单场淘汰制下弱胜强爆冷概率的统计分析为研究核心,系统构建分析模型并进行实证检验,力图从数据与方法层面揭示爆冷现象背后的规律与机制。文章首先界定“弱”“强”球队的量化标准与爆冷的统计内涵,其次引入概率论与回归分析等方法构建爆冷概率模型,再结合多项真实赛事数据进行实证检验,最后从赛制特征、心理因素与模型应用价值等角度进行综合讨论。通过理论建模与实证分析相结合,本文不仅深化了对杯赛爆冷现象的理解,也为赛事预测、竞技决策及体育管理提供了有价值的量化参考。
在现代竞技体育中,杯赛单场淘汰制被广泛应用于足球、篮球等项目,其核心特征是“一场定胜负”。相较于联赛制的长期稳定性,单场淘汰更容易受到偶然因素的影响,从而为弱队战胜强队创造了现实条件。这种制度性特征使得爆冷现象成为统计分析中一个极具研究价值的课题。
从研究背景看,爆冷并非完全随机事件,而是多种因素共同作用的结果,包括实力差距、临场状态、战术选择以及心理压力等。传统舆论往往将爆冷归因于“运气”,但统计学视角认为,运气本身也可以被概率化、模型化,从而纳入科学分析框架。
在问题界定层面,本文首先明确“弱队”与“强队”的划分标准,通常基于历史胜率、积分排名或ELO评分等量化指标。同时,“爆冷”被定义为在赛前显著不被看好的球队最终获胜的事件。通过清晰界定研究对象,为后续模型构建奠定基础。
此外,研究问题不仅关注爆冷是否发生,更关注其发生的概率水平及变化规律。通过统计分析探讨这些概率如何随赛制、实力差距与外部条件变化,是本文的核心研究目标之一。
在模型构建方面,本文以概率论为基础,将单场比赛结果视为二项分布事件,即胜或负。通过引入先验实力差距指标,将比赛结果的发生概率与球队相对实力联系起来,从而形成基础爆冷概率模型。
28圈入口进一步地,采用Logistic回归模型对爆冷事件进行刻画,将实力差距、主客场因素、赛程密集度等变量作为自变量,爆冷结果作为因变量。该模型能够有效处理非线性关系,适合分析胜负结果的概率变化。
为了增强模型解释力,本文还引入随机效应项,用以刻画不可观测因素,如临场发挥和裁判尺度。这一改进使模型在理论上更贴近真实比赛环境,也为后续实证检验提供了更稳健的工具。
模型构建过程中强调可解释性与可操作性的平衡,既保证统计推断的严谨性,又避免过度复杂化,从而使模型在实践中具有推广价值。
在实证分析阶段,本文选取多个赛季的杯赛比赛数据作为样本,涵盖不同国家和赛事层级,以增强研究结论的普适性。数据主要包括比赛结果、球队排名、历史交锋记录等关键变量。
通过对样本数据进行描述性统计,可以初步观察到弱胜强事件在单场淘汰制中并不罕见,其发生频率明显高于联赛制。这一现象从数据层面验证了研究问题的重要性。
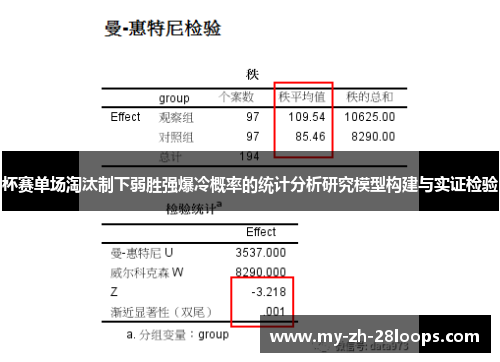
在检验方法上,本文利用回归分析对模型参数进行估计,并通过显著性检验判断各因素对爆冷概率的影响程度。同时,采用交叉验证方法检验模型的预测能力,确保结果的稳健性。
实证结果表明,实力差距越小,爆冷概率越高,而主客场因素和赛程压力也对结果产生显著影响。这些发现为理论分析提供了有力的数据支持。
从结果解释角度看,杯赛单场淘汰制本身放大了随机波动,使得弱队在短期内更容易通过集中防守或战术突袭取得胜利。这种制度性特征是爆冷高发的根本原因。
心理因素同样不可忽视。强队往往背负更大的胜负压力,而弱队则以“挑战者”心态应战,这种心理不对称在单场决胜环境下可能显著影响比赛结果。
在应用价值方面,本文构建的统计模型可为赛事预测提供量化参考,帮助媒体、俱乐部及管理机构更理性地评估比赛风险。同时,该模型也可扩展应用于其他具有淘汰特征的竞技或决策场景。
通过理论与实践的结合,研究成果不仅丰富了体育统计分析的研究内容,也为理解不确定性提供了新的视角。
总结:
总体而言,本文围绕杯赛单场淘汰制下弱胜强爆冷概率这一核心问题,从研究背景、模型构建、实证检验到结果解释进行了系统分析。通过统计模型的引入,爆冷现象不再只是经验描述,而是可以被量化和预测的概率事件。
研究表明,单场淘汰制通过放大偶然性与心理效应,显著提高了弱队取胜的可能性。未来研究可在更大样本和更多变量基础上进一步完善模型,从而不断提升对竞技不确定性的理解与应用水平。